|
Retour à la page d'accueil du site Daniel Raimboux Tours DR : Principe - Calculs - Dessins
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
PRINCIPE |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Une tour est formée de la superposition de plusieurs « tronçons ». Chaque tronçon est un solide formé de deux bases horizontales et de faces latérales.
Chaque base est un polygone régulier (côtés égaux, angles égaux, inscriptible dans un cercle). Tous les polygones réguliers ont la même mesure de côté.
La base supérieure d’un tronçon a un côté de moins que la base inférieure. La base supérieure du premier tronçon (base de la tour) est la base inférieure du 2ème tronçon, et ainsi de suite, en montant.
Le dernier tronçon a pour base inférieure un triangle équilatéral et pour base supérieure un pseudo polygone de deux côtés et deux sommets soit un segment.
Tous les polygones réguliers ont leurs centres alignés verticalement.
Chaque polygone est tourné dans son plan, autour de son centre, de sorte qu’un de ses côtés soit, dans l’espace, parallèle à un côté du polygone inférieur et un côté du polygone supérieur. La face latérale de chaque tronçon reliant ces deux côtés parallèles est donc un rectangle.
La hauteur de chaque tronçon est définie de sorte que toutes les faces rectangulaires des tronçons (définies ci-dessus) soient coplanaires et forment ensemble un grand rectangle incliné du bas en haut de la tour.
De ce fait, les tronçons n’ont pas la même hauteur ; ils sont de plus en plus hauts en s’élevant, créant ainsi pour la tour une sorte d’« accélération » vers le haut.
Pour chaque tronçon, les arêtes latérales joignent les sommets du polygone inférieur au polygone supérieur. Celui-ci a un sommet de moins. Il y a donc deux arêtes qui, partant de deux sommets voisins du bas se rejoignent en un même sommet supérieur, formant un « triangle de réduction ».
Chaque tronçon possède donc une face rectangulaire (plane), une face triangulaire (plane aussi) et une à plusieurs faces gauches, non planes, mais « réglées ».
Ces faces gauches relient dans l’espace deux arêtes latérales qui ne sont pas coplanaires. On les engendre par une droite qui reste parallèle au sol (horizontale) en montant du côté du bas au côté du haut en s’appuyant sur deux arêtes latérales voisines.
Pour chaque tronçon, le choix de l’organisation spatiale des faces a été le suivant : Vu de dessus, dans le sens antihoraire on a, successivement, la face rectangulaire, la ou les faces gauches, puis le triangle de réduction qui rejoint la face rectangulaire.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L’aspect général de la tour est donc le suivant :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
CALCULS |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
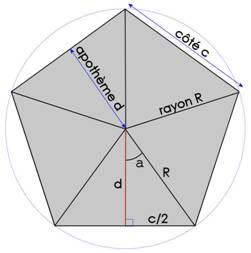
Exemple de polygone : Le pentagone régulier
Le rayon R et l’apothème d se déduisent du côté c et de l’angle a qui dépend du nombre de côtés : Nombre de côtés : 5 a = 360° / 5 x 2 2π / 5 x 2 π / 5
R = c / 2 sin (π / 5) d = c / 2 tan (π / 5)
Généralisation à n côtés :
R = c / 2 sin (π / n) d = c / 2 tan (π / n)
Exemple pour un côté de 10 cm :
|
|
Les hauteurs des tronçons se déduisent des apothèmes des polygones (d) et de la hauteur totale de la tour (H).
Exemple ; tour DR8 : le polygone de base est un octogone (n=8)
Les hauteurs partielles cumulées depuis le haut sont indicées par le nombre de côtés du polygone de base du tronçon inférieur.
Les triangles ont leurs dimensions proportionnelles.
h3 h4 h5 h6 h7 h8 d3 d4 d5 d6 d7 d8
avec d8 = demi largeur de la tour et h8 = H, hauteur de la tour.
h8 / d8 est la moitié du rapport hauteur / largeur, c'est-à-dire « l’élancement » de la tour.
Exemple d’une tour DR 8 de largeur 30 cm à la base et de hauteur 2m (d’où le côté égal à 12,4 cm) :
Généralisation : Les hauteurs cumulées ne dépendent que de H et de n selon la formule : hi = H x [(tan π/n)/(tan π/i)]
i allant de 3 à n n étant le nombre de côtés de la base de la tour
Daniel Raimboux – janvier 2010 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
DESSINS DR 8 (le polygone de base est un octogone) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
DESSINS DR 10 (le polygone de base est un décagone) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||